Система тел и пружин

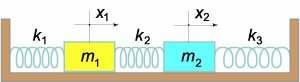
Система тел, соединенных между собой пружинами, является классической системой с несколькими степенями свободы. Так, например, система двух тел с тремя пружинами имеет две степени свободы. Это означает, что ее конфигурацию можно описать двумя обобщенными координатами, в качестве которых удобно взять смещения первого и второго тела от положения равновесия.

Движение связанных тел описывается системой двух дифференциальных уравнений $2$-го порядка. В простейшем случае можно пренебречь силами трения и сопротивления воздуха и учитывать лишь силы упругости, которые подчиняются закону Гука. Оказывается, даже такая упрощенная система обладает нетривиальными динамическими свойствами. В целом, характер ее движения определяется двумя собственными частотами, которые зависят от параметров системы (т.е. от масс тел и коэффициентов жесткости пружин). Кроме того, движение тел существенно зависит от начальных условий. Влияние этих факторов можно изучить с помощью представленной ниже анимации. Несмотря на разнообразный характер движения, система является линейной и, следовательно, допускает точное решение. Наша дальнейшая цель состоит в том, чтобы построить это решение, детально описывая все шаги.

Данная система схематически изображена на рисунке $1.$ Она состоит из двух тел, массы которых равны ${m_1}$ и ${m_2},$ и трех пружин с коэффициентами жесткости ${k_1},$ ${k_2},$ ${k_3}.$ Смещение тел от положений равновесия определяется координатами ${x_1}$ и ${x_2}.$ Составим уравнения движения. Это можно сделать непосредственно с помощью второго закона Ньютона или используя Лагранжев формализм. Мы воспользуемся вторым методом. Запишем выражения для кинетической и потенциальной энергии системы. Заметим, что в данной идеальной системе полная энергия сохраняется. $${T = \frac{{{m_1}\dot x_1^2}}{2} + \frac{{{m_2}\dot x_2^2}}{2},}\;\; {V = \frac{{{k_1}x_1^2}}{2} + \frac{{{k_2}{{\left( {{x_2} - {x_1}} \right)}^2}}}{2} + \frac{{{k_3}x_2^2}}{2}.}$$ Здесь точками, как это принято в механике, обозначены первые производные координат, т.е. скорости тел. Лагранжиан системы записывается в следующем виде: $${L = T - V } = {\frac{1}{2}\left[ {{m_1}\dot x_1^2 + {m_2}\dot x_2^2 - {k_1}x_1^2 - {k_2}{{\left( {{x_2} - {x_1}} \right)}^2} - {k_3}x_2^2} \right].}$$ Составим дифференциальные уравнения Лагранжа: $${\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot x}_i}}} = \frac{{\partial L}}{{\partial {x_i}}}\;\;\;\text{или}}\;\;\; {\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot x}_1}}} = \frac{{\partial L}}{{\partial {x_1}}},}\;\; {\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{\dot x}_2}}} = \frac{{\partial L}}{{\partial {x_2}}}.}$$ Найдем частные производные: $${\frac{{\partial L}}{{\partial {{\dot x}_1}}} = \frac{1}{2} \cdot 2{m_1}{\dot x_1} = {m_1}{\dot x_1},}\;\; {\frac{{\partial L}}{{\partial {x_1}}} = \frac{1}{2}\left[ { - 2{k_1}{x_1} + 2{k_2}\left( {{x_2} - {x_1}} \right)} \right] } = { - {k_1}{x_1} + {k_2}\left( {{x_2} - {x_1}} \right),}$$ $${\frac{{\partial L}}{{\partial {{\dot x}_2}}} = \frac{1}{2} \cdot 2{m_2}{\dot x_2} = {m_2}{\dot x_2},}\;\; {\frac{{\partial L}}{{\partial {x_2}}} = \frac{1}{2}\left[ { - 2{k_2}\left( {{x_2} - {x_1}} \right) - 2{k_2}{x_2}} \right] } = { - {k_2}\left( {{x_2} - {x_1}} \right) - {k_3}{x_2}.}$$ В результате получаем следующую систему уравнений, описывающую движение тел: $${\left\{ \begin{array}{l} {m_1}{{\ddot x}_1} = - {k_1}{x_1} + {k_2}\left( {{x_2} - {x_1}} \right)\\ {m_2}{{\ddot x}_2} = - {k_2}\left( {{x_2} - {x_1}} \right) - {k_3}{x_2} \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {{\ddot x}_1} = - \frac{{{k_1}}}{{{m_1}}}{x_1} + \frac{{{k_2}}}{{{m_1}}}{x_2} - \frac{{{k_2}}}{{{m_1}}}{x_1}\\ {{\ddot x}_2} = - \frac{{{k_2}}}{{{m_2}}}{x_2} + \frac{{{k_2}}}{{{m_2}}}{x_1} - \frac{{{k_3}}}{{{m_2}}}{x_2} \end{array} \right.,}\;\; {\Rightarrow \left\{ \begin{array}{l} {{\ddot x}_1} = - \frac{{{k_1} + {k_2}}}{{{m_1}}}{x_1} + \frac{{{k_2}}}{{{m_1}}}{x_2}\\ {{\ddot x}_2} = \frac{{{k_2}}}{{{m_2}}}{x_1} - \frac{{{k_2} + {k_3}}}{{{m_2}}}{x_2} \end{array} \right..}$$ Эту систему можно представить в матричной форме: $${\mathbf{\ddot X} = K\mathbf{X},\;\;\text{где}}\;\; {\mathbf{X} = \left( {\begin{array}{*{20}{c}} {{x_1}}\\ {{x_2}} \end{array}} \right),}\;\; {\mathbf{\ddot X} = \left( {\begin{array}{*{20}{c}} {{{\ddot x}_1}}\\ {{{\ddot x}_2}} \end{array}} \right),}\;\; {K = \left( {\begin{array}{*{20}{c}} { - \frac{{{k_1} + {k_2}}}{{{m_1}}}}&{\frac{{{k_2}}}{{{m_1}}}}\\ {\frac{{{k_2}}}{{{m_2}}}}&{ - \frac{{{k_2} + {k_3}}}{{{m_2}}}} \end{array}} \right).}$$ Будем искать решение $\mathbf{X}\left( t \right)$ в форме гармонических колебаний, т.е. в виде $$\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{B_1}}\\ {{B_2}} \end{array}} \right){e^{i\omega t}},$$ где ${{B_1}},$ ${{B_2}}$ − амплитуды колебаний тел, $\omega$ − собственные частоты колебаний, подлежащие определению.

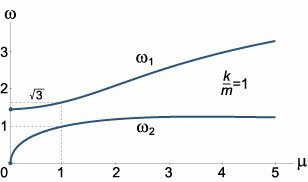
Подставляя пробные функции ${x_1}\left( t \right),$ ${x_2}\left( t \right)$ в матричное уравнение, получаем характеристическое уравнение для определения собственных частот колебаний: $${\det \left( {K + {\omega ^2}I} \right) = 0,}\;\; {\Rightarrow \left| {\begin{array}{*{20}{c}} { - \frac{{{k_1} + {k_2}}}{{{m_1}}} + {\omega ^2}}&{\frac{{{k_2}}}{{{m_1}}}}\\ {\frac{{{k_2}}}{{{m_2}}}}&{ - \frac{{{k_2} + {k_3}}}{{{m_2}}} + {\omega ^2}} \end{array}} \right| = 0,}\;\; {\Rightarrow \left( {{\omega ^2} - \frac{{{k_1} + {k_2}}}{{{m_1}}}} \right)\left( {{\omega ^2} - \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right) - \frac{{k_2^2}}{{{m_1}{m_2}}} = 0,}\;\; {\Rightarrow {\omega ^4} - \frac{{{k_1} + {k_2}}}{{{m_1}}}{\omega ^2} - \frac{{{k_2} + {k_3}}}{{{m_2}}}{\omega ^2} } + {\frac{{\left( {{k_1} + {k_2}} \right)\left( {{k_2} + {k_3}} \right)}}{{{m_1}{m_2}}} - \frac{{k_2^2}}{{{m_1}{m_2}}} = 0,}\;\; {\Rightarrow {\omega ^4} - \left( {\frac{{{k_1} + {k_2}}}{{{m_1}}} + \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right){\omega ^2} } + {\frac{{\left( {{k_1} + {k_2}} \right)\left( {{k_2} + {k_3}} \right)}}{{{m_1}{m_2}}} - \frac{{k_2^2}}{{{m_1}{m_2}}} = 0.}$$ Решая это биквадратное уравнение, находим собственные частоты колебаний. Вычислим сначала дискриминант: $${D = {\left( {\frac{{{k_1} + {k_2}}}{{{m_1}}} + \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right)^2} } - {4\left[ {\frac{{\left( {{k_1} + {k_2}} \right)\left( {{k_2} + {k_3}} \right)}}{{{m_1}{m_2}}} - \frac{{k_2^2}}{{{m_1}{m_2}}}} \right] } = {{\left( {\frac{{{k_1} + {k_2}}}{{{m_1}}}} \right)^2} + {\left( {\frac{{{k_2} + {k_3}}}{{{m_2}}}} \right)^2} } + {\frac{{2\left( {{k_1} + {k_2}} \right)\left( {{k_2} + {k_3}} \right)}}{{{m_1}{m_2}}} } - {\frac{{4\left( {{k_1} + {k_2}} \right)\left( {{k_2} + {k_3}} \right)}}{{{m_1}{m_2}}} } + {\frac{{4k_2^2}}{{{m_1}{m_2}}} } = {{\left( {\frac{{{k_1} + {k_2}}}{{{m_1}}} - \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right)^2} } + {\frac{{4k_2^2}}{{{m_1}{m_2}}}.}$$ Тогда квадраты собственных частот будут описываться формулой $${{\omega ^2} } = {\frac{1}{2}\left[ {\left( {\frac{{{k_1} + {k_2}}}{{{m_1}}} + \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right) \pm \sqrt {{{\left( {\frac{{{k_1} + {k_2}}}{{{m_1}}} - \frac{{{k_2} + {k_3}}}{{{m_2}}}} \right)}^2} + \frac{{4k_2^2}}{{{m_1}{m_2}}}} } \right].}$$ Далее, чтобы избежать громоздких формул, рассмотрим более простой случай, когда жесткость всех пружин одинакова: ${k_1} = {k_2} = {k_3} = k.$ Кроме того, введем отношение масс тел: $\mu = \large\frac{{{m_2}}}{{{m_1}}}\normalsize.$ Тогда формула для квадрата частот колебаний принимает такой вид: $${{\omega ^2} } = {\frac{1}{2}\left[ {\left( {\frac{{2k}}{{{m_1}}} + \frac{{2k}}{{{m_2}}}} \right) \pm \sqrt {{{\left( {\frac{{2k}}{{{m_1}}} - \frac{{2k}}{{{m_2}}}} \right)}^2} + \frac{{4{k^2}}}{{{m_1}{m_2}}}} } \right] } = {k\left[ {\left( {\frac{1}{{{m_1}}} + \frac{1}{{{m_2}}}} \right) \pm \sqrt {{{\left( {\frac{1}{{{m_1}}} - \frac{1}{{{m_2}}}} \right)}^2} + \frac{1}{{{m_1}{m_2}}}} } \right],}\;\; {\Rightarrow {\omega ^2}{m_2} = k\left[ {\left( {\frac{{{m_2}}}{{{m_1}}} + \frac{{{m_2}}}{{{m_2}}}} \right) \pm \sqrt {{{\left( {\frac{{{m_2}}}{{{m_1}}} - \frac{{{m_2}}}{{{m_2}}}} \right)}^2} + \frac{{m_2^2}}{{{m_1}{m_2}}}} } \right] } = {k\left[ {\mu + 1 \pm \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right],}\;\; {\Rightarrow {\omega ^2} = \frac{k}{{{m_2}}}\left[ {\mu + 1 \pm \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right].}$$ Полученное соотношение описывает $2$ собственных частоты: ${\omega _1}$ (со знаком "плюс") и ${\omega _2}$ (со знаком "минус"). Зависимости частот ${\omega _1},$ ${\omega _2}$ от отношения масс $\mu$ показаны на рисунке $2.$ В случае равных масс $\left( {\mu = 1} \right)$ собственные частоты колебаний будут описываться следующими компактными формулами: $${\omega _1} = \sqrt {\frac{{3k}}{m}} ,\;\;{\omega _2} = \sqrt {\frac{k}{m}} .$$ Заметим, что частоты ${\omega _1},$ ${\omega _2}$ всегда являются действительными числами. Это следует из общих физических соображений. Действительно, при мнимой частоте возникла бы утечка энергии, что противоречило бы условию сохранения энергии в системе. Данный факт, однако, можно установить и чисто математическим путем. В самом деле, вопрос возникает лишь для частоты ${\omega _2}.$ Условие неотрицательности для $\omega _2^2$ выглядит так: $${\omega _2^2 > 0,}\;\; {\Rightarrow \mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } > 0,}\;\; {\Rightarrow \mu + 1 > \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } .}$$ Здесь левая часть неравенства и выражение под корнем в правой части всегда положительны. После возведения обеих частей неравенства в квадрат получаем: $$\require{cancel} {{\left( {\mu + 1} \right)^2} > {\left( {\mu - 1} \right)^2} + \mu ,}\;\; {\Rightarrow \cancel{\mu ^2} + 2\mu + \cancel{1} > \cancel{\mu ^2} - 2\mu + \cancel{1} + \mu ,}\;\; {\Rightarrow 3\mu > 0,}\;\; {\Rightarrow \mu > 0,}$$ что всегда выполняется.

Найдем собственный вектор ${\mathbf{H}_1} = {\left( {{H_{11}},{H_{21}}} \right)^T}$ (верхний индекс $^T$ обозначает операцию транспонирования), соответствующий частоте ${\omega _1}.$ Он определяется из матрично-векторного уравнения $$\left( {K + \omega _1^2I} \right){\mathbf{H}_1} = \mathbf{0}.$$ Следовательно, $${\left( {\begin{array}{*{20}{c}} { - \frac{{2k}}{{{m_1}}} + \frac{k}{{{m_2}}}\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]}&{\frac{k}{{{m_1}}}}\\ {\frac{k}{{{m_2}}}}&{ - \frac{{2k}}{{{m_1}}} + \frac{k}{{{m_2}}}\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{H_{11}}}\\ {{H_{21}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( { - \frac{2}{{{m_1}}} + \frac{1}{{{m_2}}}\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right){H_{11}} + \frac{1}{{{m_1}}}{H_{21}} = 0}\\ {\frac{1}{{{m_2}}}{H_{11}} + \left( { - \frac{2}{{{m_1}}} + \frac{1}{{{m_2}}}\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right){H_{21}} = 0} \end{array}} \right..}$$ В последней системе оба уравнения являются линейно зависимыми (поскольку определитель матрицы $K$ равен нулю при ${\omega ^2} = \omega _1^2$). Поэтому, координаты собственного вектора ${\mathbf{H}_1}$ можно выразить, например, из первого уравнения. Пусть ${H_{11}} = 1.$ Тогда $${{H_{21}} = {m_1}\left( {\frac{2}{{{m_1}}} - \frac{1}{{{m_2}}}\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right) } = {2 - \frac{1}{\mu }\left[ {\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right] } = {1 - \frac{{1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu } } = {\frac{{\mu - 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }.}$$ Таким образом, вектор ${\mathbf{H}_1}$ имеет следующие координаты: $${\mathbf{H}_1} = \left( {\begin{array}{*{20}{c}} {{H_{11}}}\\ {{H_{21}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{\mu - 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }} \end{array}} \right).$$ Аналогично можно определить собственный вектор ${\mathbf{H}_2} = {\left( {{H_{12}},{H_{22}}} \right)^T},$ соответствующий частоте ${\omega _2}.$ В этом случае для ${\mathbf{H}_2}$ имеем уравнение $$\left( {K + \omega _2^2 I} \right){\mathbf{H}_2} = \mathbf{0}.$$ В развернутом виде оно записывается как $${\left( {\begin{array}{*{20}{c}} { - \frac{{2k}}{{{m_1}}} + \frac{k}{{{m_2}}}\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]}&{\frac{k}{{{m_1}}}}\\ {\frac{k}{{{m_2}}}}&{ - \frac{{2k}}{{{m_1}}} + \frac{k}{{{m_2}}}\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{H_{12}}}\\ {{H_{22}}} \end{array}} \right) = \mathbf{0},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {\left( { - \frac{2}{{{m_1}}} + \frac{1}{{{m_2}}}\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right){H_{12}} + \frac{1}{{{m_1}}}{H_{22}} = 0}\\ {\frac{1}{{{m_2}}}{H_{12}} + \left( { - \frac{2}{{{m_1}}} + \frac{1}{{{m_2}}}\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right){H_{22}} = 0} \end{array}} \right..}$$ Полагая ${H_{12}} = 1,$ из первого уравнения найдем координату ${H_{22}}:$ $${{H_{22}} = {m_1}\left( {\frac{2}{{{m_1}}} - \frac{1}{{{m_2}}}\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]} \right) } = {2 - \frac{1}{\mu }\left[ {\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right] } = {1 - \frac{{1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu } } = {\frac{{\mu - 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }.}$$ Следовательно, $${\mathbf{H}_2} = \left( {\begin{array}{*{20}{c}} {{H_{12}}}\\ {{H_{22}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{\mu - 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }} \end{array}} \right).$$ После того, как собственные частоты ${\omega _1},{\omega _2}$ и собственные векторы ${\mathbf{H}_1},$ ${\mathbf{H}_2}$ найдены, можно записать общее решение системы. Учтем, что каждый из собственных векторов соответствует квадрату собственной частоты, т.е. двум значениям частот с противоположными знаками. Вектору ${\mathbf{H}_1}$ соответствуют две частоты $\pm{\omega _1},$ а вектору ${\mathbf{H}_2}$ − частоты $\pm{\omega _2}.$ В результате общее комплексное решение представляется в виде суммы четырех слагаемых: $${\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) } = {{C_1}{e^{i{\omega _1}t}}{\mathbf{H}_1} + {C_2}{e^{ - i{\omega _1}t}}{\mathbf{H}_1} } + {{C_3}{e^{i{\omega _2}t}}{\mathbf{H}_2} + {C_4}{e^{ - i{\omega _2}t}}{\mathbf{H}_2},}$$ где ${C_1}, \ldots ,{C_4}$ − постоянные (в данном случае комплексные) числа. Пусть данные числа записываются в виде $${{C_1} = {\alpha _1} + i{\beta _1},\;\;{C_2} = {\alpha _2} + i{\beta _2},}\;\; {{C_3} = {\alpha _3} + i{\beta _3},}\;\; {{C_4} = {\alpha _4} + i{\beta _4}.}$$ Чтобы величины ${x_1}\left( t \right),{x_2}\left( t \right)$ оставались действительными при любом значении $t,$ необходимо, чтобы выполнялись соотношения $${{C_1} = {\bar C_2},\;\; \Rightarrow {\alpha _1} + i{\beta _1} = {\alpha _2} - i{\beta _2},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{\alpha _1} = {\alpha _2}}\\ {{\beta _1} = - {\beta _2}} \end{array}} \right.,}$$ $${{C_3} = {{\bar C}_4},\;\; \Rightarrow {\alpha _3} + i{\beta _3} = {\alpha _4} - i{\beta _4},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{\alpha _3} = {\alpha _4}}\\ {{\beta _3} = - {\beta _4}} \end{array}} \right..}$$ Тогда мнимые части общего решения будут сокращаться. Действительно, $${\mathbf{X}\left( t \right) = \left( {{\alpha _1} + i{\beta _1}} \right){e^{i{\omega _1}t}}{\mathbf{H}_1} } + {\left( {{\alpha _2} + i{\beta _2}} \right){e^{ - i{\omega _1}t}}{\mathbf{H}_1} } + {\left( {{\alpha _3} + i{\beta _3}} \right){e^{i{\omega _2}t}}{\mathbf{H}_2} } + {\left( {{\alpha _4} + i{\beta _4}} \right){e^{ - i{\omega _2}t}}{\mathbf{H}_2} } = {{\alpha _1}\left( {{e^{i{\omega _1}t}} + {e^{ - i{\omega _1}t}}} \right){\mathbf{H}_1} } + {i{\beta _1}\left( {{e^{i{\omega _1}t}} - {e^{ - i{\omega _1}t}}} \right){\mathbf{H}_1} } + {{\alpha _3}\left( {{e^{i{\omega _2}t}} + {e^{ - i{\omega _2}t}}} \right){\mathbf{H}_2} } + {i{\beta _3}\left( {{e^{i{\omega _2}t}} - {e^{ - i{\omega _2}t}}} \right){\mathbf{H}_2}.}$$ Выражения в квадратных скобках можно упростить по формуле Эйлера: $${{e^{i\omega t}} + {e^{ - i\omega t}} } = {\cos \left( {\omega t} \right) + \cancel{i\sin \left( {\omega t} \right)} } + {\cos \left( { - \omega t} \right) + \cancel{i\sin \left( { - \omega t} \right)} } = {2\cos \left( {\omega t} \right),}$$ $${{e^{i\omega t}} - {e^{ - i\omega t}} } = {\cancel{\cos \left( {\omega t} \right)} + i\sin \left( {\omega t} \right) } - {\cancel{\cos \left( { - \omega t} \right)} - i\sin \left( { - \omega t} \right) } = {2i\sin \left( {\omega t} \right).}$$ Следовательно, $${\mathbf{X}\left( t \right) = 2\left[ {{\alpha _1}\cos \left( {{\omega _1}t} \right) - {\beta _1}\sin\left( {{\omega _1}t} \right)} \right]{\mathbf{H}_1} } + {2\left[ {{\alpha _3}\cos \left( {{\omega _2}t} \right) - {\beta _3}\sin\left( {{\omega _2}t} \right)} \right]{\mathbf{H}_2}.}$$ Далее удобно ввести фазовые углы ${\varphi _1},{\varphi _2}$ и воспользоваться тригонометрической формулой $$\cos \left( {\omega t + \varphi } \right) = \cos \omega t\cos \varphi - \sin \omega t\sin \varphi .$$ В результате общее решение будет записываться в следующем виде: $${\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) } = {{A_1}\cos \left( {{\omega _1}t + {\varphi _1}} \right){\mathbf{H}_1} } + {{A_2}\cos \left( {{\omega _2}t + {\varphi _2}} \right){\mathbf{H}_2},}$$ где действительные постоянные ${A_1},$ ${A_2},$ ${\varphi _1},$ ${\varphi _2}$ зависят от начальных смещений и начальных скоростей тел, а собственные частоты ${\omega_1},$ ${\omega_2}$ и собственные векторы ${\mathbf{H}_1},$ ${\mathbf{H}_2}$ определяются соотношениями $${\omega _{1,2}} = \sqrt {\frac{k}{{{m_2}}}} {\left[ {\mu + 1 \pm \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } } \right]^{\large\frac{1}{2}\normalsize}},$$ $${{\mathbf{H}_1} = \left( {\begin{array}{*{20}{c}} {{H_{11}}}\\ {{H_{21}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{\mu + 1 - \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }} \end{array}} \right),}\;\;\; {{\mathbf{H}_2} = \left( {\begin{array}{*{20}{c}} {{H_{12}}}\\ {{H_{22}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ {\frac{{\mu + 1 + \sqrt {{{\left( {\mu - 1} \right)}^2} + \mu } }}{\mu }} \end{array}} \right).}$$ Закон изменения скоростей тел находится путем дифференцирования общего решения: $${\mathbf{\dot X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{{\dot x}_1}\left( t \right)}\\ {{{\dot x}_2}\left( t \right)} \end{array}} \right) } = { - {A_1}{\omega _1}\sin \left( {{\omega _1}t + {\varphi _1}} \right){\mathbf{H}_1} } - {{A_2}{\omega _2}\sin\left( {{\omega _2}t + {\varphi _2}} \right){\mathbf{H}_2}.}$$ Отсюда видно, что если в начальный момент $t = 0$ скорости тел равны нулю, то фазовые углы ${\varphi _1},$ ${\varphi _2}$ также равны нулю. Далее будем рассматривать именно такой случай. Общее решение представляет собой сумму двух гармоник с частотами ${\omega_1},$ ${\omega_2}:$ $${\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) } = {{A_1}\cos \left( {{\omega _1}t} \right){\mathbf{H}_1} + {A_2}\cos \left( {{\omega _2}t} \right){\mathbf{H}_2}.}$$ Вычислим постоянные ${A_1},$ ${A_2}$ в зависимости от начальных смещений. Пусть $$\mathbf{X}\left( 0 \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( 0 \right)}\\ {{x_2}\left( 0 \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{x_{10}}}\\ {{x_{20}}} \end{array}} \right).$$ Следовательно, $${\mathbf{X}\left( 0 \right) = \left( {\begin{array}{*{20}{c}} {{x_{10}}}\\ {{x_{20}}} \end{array}} \right) = {A_1}{\mathbf{H}_1} + {A_2}{\mathbf{H}_2},}\;\; {\Rightarrow \left\{ {\begin{array}{*{20}{l}} {{A_1}{H_{11}} + {A_2}{H_{12}} = {x_{10}}}\\ {{A_1}{H_{21}} + {A_2}{H_{22}} = {x_{20}}} \end{array}} \right..}$$ Эту алгебраическую систему можно решить по формулам Крамера: $${\Delta = \left| {\begin{array}{*{20}{c}} {{H_{11}}}&{{H_{12}}}\\ {{H_{21}}}&{{H_{22}}} \end{array}} \right| = {H_{11}}{H_{22}} - {H_{12}}{H_{21}},}\;\;\; {{\Delta _1} = \left| {\begin{array}{*{20}{c}} {{x_{10}}}&{{H_{12}}}\\ {{x_{20}}}&{{H_{22}}} \end{array}} \right| = {x_{10}}{H_{22}} - {x_{20}}{H_{12}},}\;\;\; {{\Delta _2} = \left| {\begin{array}{*{20}{c}} {{H_{11}}}&{{x_{10}}}\\ {{H_{21}}}&{{x_{20}}} \end{array}} \right| = {x_{20}}{H_{11}} - {x_{10}}{H_{21}},}$$ $${\Rightarrow {A_1} = \frac{{{\Delta _1}}}{\Delta } = \frac{{{x_{10}}{H_{22}} - {x_{20}}{H_{12}}}}{{{H_{11}}{H_{22}} - {H_{12}}{H_{21}}}},}\;\;\; {{A_2} = \frac{{{\Delta _2}}}{\Delta } = \frac{{{x_{20}}{H_{11}} - {x_{10}}{H_{21}}}}{{{H_{11}}{H_{22}} - {H_{12}}{H_{21}}}}.}$$ Итак, при начальных условиях $$\mathbf{X}\left( 0 \right) = \left( {\begin{array}{*{20}{c}} {{x_{10}}}\\ {{x_{20}}} \end{array}} \right),\;\;\mathbf{\dot X}\left( 0 \right) = \left( {\begin{array}{*{20}{c}} 0\\ 0 \end{array}} \right)$$ получаем следующую формулу общего решения: $${\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) } = {{A_1}\cos \left( {{\omega _1}t} \right){\mathbf{H}_1} } + {{A_2}\cos \left( {{\omega _2}t} \right){\mathbf{H}_2},}$$ где постоянные ${A_1},$ ${A_2}$ равны $${{A_1} = \frac{{{x_{10}}{H_{22}} - {x_{20}}{H_{12}}}}{{{H_{11}}{H_{22}} - {H_{12}}{H_{21}}}},}\;\;\; {{A_2} = \frac{{{x_{20}}{H_{11}} - {x_{10}}{H_{21}}}}{{{H_{11}}{H_{22}} - {H_{12}}{H_{21}}}},}$$ а собственные векторы и собственные частоты выражаются через отношение масс $\mu,$ массу второго тела ${m_2}$ и коэффициент жесткости пружин $k$ по приведенным выше формулам.

Полученные выражения значительно упрощаются, когда массы обоих тел одинаковы. Полагая $\mu = 1,$ получаем следующие формулы (при тех же самых начальных условиях): $${\mathbf{X}\left( t \right) = \left( {\begin{array}{*{20}{c}} {{x_1}\left( t \right)}\\ {{x_2}\left( t \right)} \end{array}} \right) } = {{A_1}\cos \left( {{\omega _1}t} \right){\mathbf{H}_1} } + {{A_2}\cos \left( {{\omega _2}t} \right){\mathbf{H}_2},\;\;\text{где}}$$ $${{\omega _1} = \sqrt {\frac{{3k}}{m}} ,\;\;{\omega _2} = \sqrt {\frac{k}{m}} ,}\;\; {{\mathbf{H}_1} = \left( {\begin{array}{*{20}{c}} {{H_{11}}}\\ {{H_{12}}} \end{array}} \right) = \left( {\begin{array}{*{20}{r}} 1\\ { - 1} \end{array}} \right),}\;\; {{\mathbf{H}_2} = \left( {\begin{array}{*{20}{c}} {{H_{12}}}\\ {{H_{22}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1\\ 1 \end{array}} \right),}\;\; {{A_1} = \frac{{{x_{10}} - {x_{20}}}}{2},\;\;{A_2} = \frac{{{x_{10}} + {x_{20}}}}{2}.}$$ Следовательно, в случае одинаковых масс и одинаковых коэффициентов жесткости законы движения тел определяются соотношениями: $$\left\{ \begin{array}{l} {x_1}\left( t \right) = \frac{{{x_{10}} + {x_{20}}}}{2}\cos \left( {\sqrt {\frac{k}{m}} t} \right) + \frac{{{x_{10}} - {x_{20}}}}{2}\cos \left( {\sqrt {\frac{{3k}}{m}} t} \right)\\ {x_2}\left( t \right) = \frac{{{x_{10}} + {x_{20}}}}{2}\cos \left( {\sqrt {\frac{k}{m}} t} \right) - \frac{{{x_{10}} - {x_{20}}}}{2}\cos \left( {\sqrt {\frac{{3k}}{m}} t} \right) \end{array} \right..$$ В начале web-страницы представлена анимация, демонстрирующая характер колебаний тел, соединенных пружинами, при различных параметрах системы $\mu,$ $k$ и начальных смещениях ${x_{10}},$ ${x_{20}}.$ В модели принято значение ${m_2} = 2\,\text{кг}.$ Коэффициент жесткости $k$ измеряется в $\large\frac{\text{Н}}{\text{м}}\normalsize.$ Смещения грузов показаны в сантиметрах в масштабе $1\,\text{см} = 1\,\text{пиксель}$ (график имеет масштаб $1\,\text{см} = 3\,\text{пикселя}.$)

Видно, что в системе наблюдаются биения, при которых энергия циклически перераспределяется от одного тела к другому. При близких начальных смещениях одного знака грузы двигаются синфазно. И наоборот, при противоположных смещениях движение происходит в противофазе.

Системы тел и пружин являются физической основой при моделировании и решении многих инженерных задач. Такого рода модели используются при проектировании строительных конструкций или, например, при разработке спортивной одежды. Разумеется, в реальных ситуациях система уравнений может быть гораздо более сложной.